Дана равнобокая трапеция ABCD с основаниями AB и CD. Известно, что окружности, вписанные в треугольники ABC и ACD, касаются диагонали AC в одной и той же точке. При этом точка касания первой окружности со стороной BC делит эту сторону пополам. Найдите отношение, в котором точка касания второй окружности со стороной AD делит эту сторону, считая от точки A.
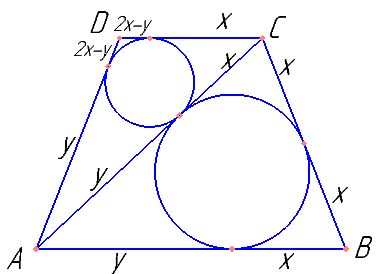
Прежде, чем решать эту задачу — разберите вот эту.
Площадь треугольника ADC, используя формулу Герона: \( x\sqrt{3y(2x-y)} \).
Площадь треугольника ACB, используя формулу Герона: \( x\sqrt{y(2x+y)} \).
Высота трапеции \( \sqrt{3x^2-y^2+2xy} \)
Площадь трапеции \( x\sqrt{3x^2-y^2+2xy} \)
Сумма площадей треугольников равна площади трапеции. Из этого можно найти, что \( y=\sqrt{3}x \).
Ответ: \( (2\sqrt{3}+3):1 \)
