Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и M и пересекает продолжение стороны CD за точку D в точке N.
а) Докажите, что AM=AN.
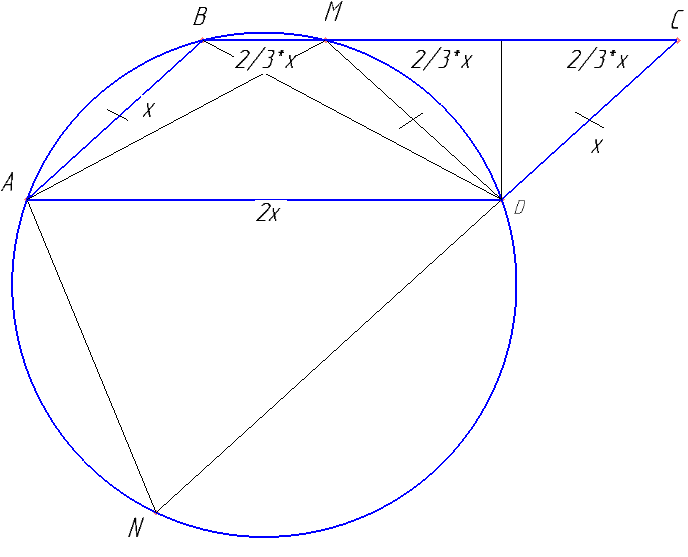
б) Найдите отношение CD:DN, если AB:BC=1:2, а cos∠BAD=\( \frac{2}{3} \).
Две параллельные прямые при пересечении с окружностью образуют 4 точки. Доказать, что эти точки являются вершинами равнобедренной трапеции.
Доказать, что угол ADM равен углу ADN.
Пусть BM=4, MC=8, CD=6. Найти DN. Пригодиться теорема о двух секущих.
Ответ:0,6
