Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK=15, KL=6, LB=5.
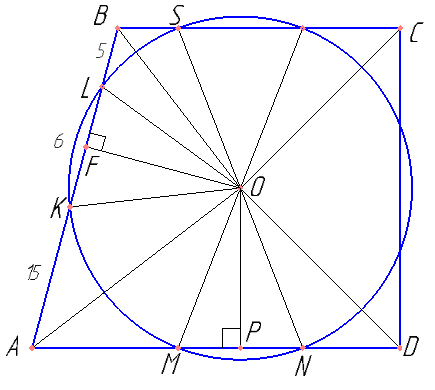
Похоже, что биссектрисы пересекаются в центре окружности. Докажем это. Доказать, что треугольники KLO и MNO равны. Доказать, что OF=OP. Доказать, что треугольника AFO и APO равны, т.е. AO — биссектриса.
Найти AM и BS.
Обосновать, что SM- высота трапеции. В прямоугольной трапеции основания равны 5 и 15, а большая боковая сторона 26. Найти высоту трапеции.
Ответ: 24.
