а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого.
б) Пусть O — точка пересечения диагоналей трапеции ABCD. Найдите расстояние от вершины C до середины отрезка OD, если BC=16 и AB=10.
В равнобедренной трапеции ABCD основание AD в три раза больше основания BC.
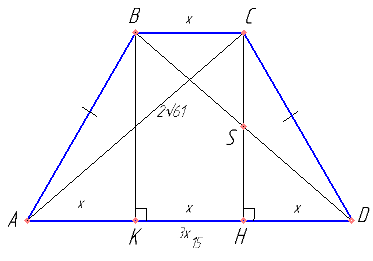
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых вдвое больше другого.
б) Найдите расстояние от вершины C до середины диагонали BD, если AD=15 и AC=2\( \sqrt{61} \).
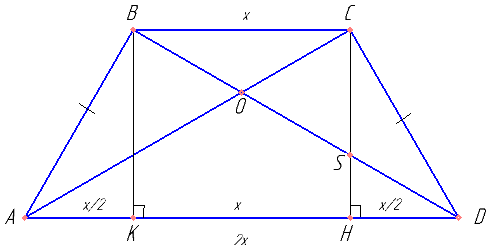
В равнобедренной трапеции ABCD проведены высоты BK и CH. Основание BC в три раза меньше AD. Пусть BC=x. Выразить черех x AK, KH, HD.
Зрительно кажется, что OS=SD. Докажем это. Пусть BO = y. Выразить через y — OD, BD. По теореме Фалеса высоты KB и HC делят диагональ в отношении BS:SD=KH:HD. Выразить через y — SD и OS.
В равнобедренной трапеции основания равны 16 и 32, а боковая сторона 10. Найти высоту трапеции.
Доказать, что треугольник BCS подобен треугольнику DHS. Найти CS.
Ответ: 4; 6.
