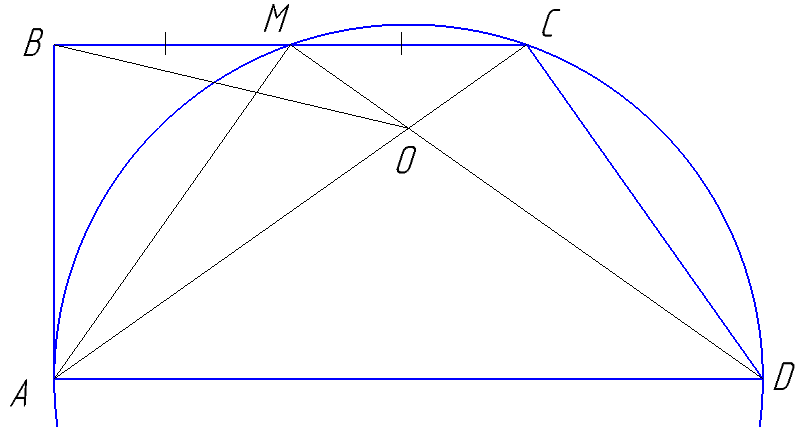
В трапеции ABCD угол BAD прямой. Окружность, построенная на большем основании AD как на диаметре, пересекает меньшее основание BC в точках C и M.
а) Докажите, что ∠BAM=∠CAD.
б) Диагонали трапеции ABCD пересекаются в точке O. Найдите площадь треугольника AOB, если AB=\( \sqrt{10} \), а BC=2BM.
Обоснуйте равенство углов BAM и ACM, ACM и CAD.
Известен только один линейный размер и соотношения отрезков – ищи подобные треугольники. (Часто помогает теорема о касательной и секущей).
Обоснуйте подобие треугольников ABC и MBA. Найти BM.
Докажите, что\( AD=3MC \), \( AO=3CO \).
В треугольнике ABC на основании AC взяли точку O, так что AO:OC=3:1. Найти отношение площадей треугольников ABC и ABO.
Ответ: \( 3,75\sqrt{2} \).
