В треугольнике ABC точки A1, B1 и C1 — середины сторон BC, AC и AB соответственно, AH — высота, ∠BAC=60, ∠BCA=45.
а) Докажите, что точки A1, B1, C1 и H лежат на одной окружности.
б) Найдите A1H, если BC=\( 2\sqrt{3} \).
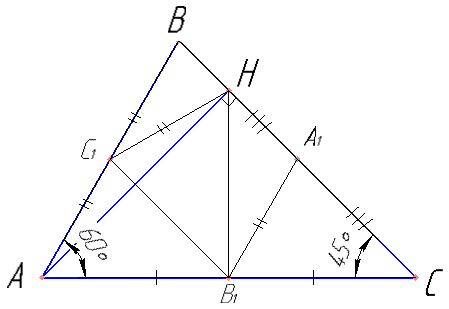
Рассчитайте все показанные на чертеже углы.
В четырехугольнике АВСD угол А равен 16°, угол В равен 29°, угол С равен 164°, угол D равен 151°. Доказать, что вокруг четырехугольника можно описать окружность.
Трапеция C1HA1B1 вписана в окружность. Большее основание C1B1 равно \( \sqrt{3} \). ∠C1HB1 =60°, ∠HB1A1=30°. Найти HA1. Примените теорему синусов.
Можно найти другое решение, но предложенное — красиво и кратко.
Ответ: 1.
