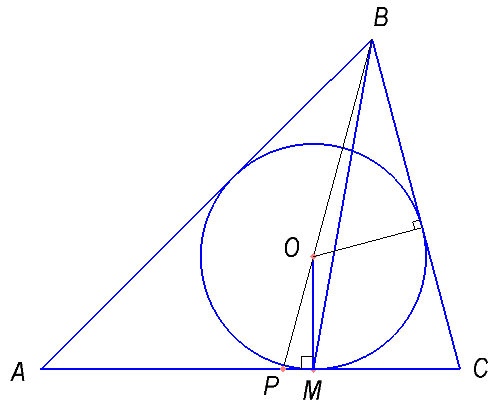
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin∠BMC, если известно, что отрезок BM в 2,5 раза больше радиуса вписанной в треугольник окружности.
Надо рассмотреть два случая — когда BM совпадает с биссектрисой и нет. Доказать, что в первом случае BM равен трем радиусам окружности. Во втором случае обосновать, что BM<BO+OM, т.е. BM меньше трех радиусов окружности.
В угол ABC величиной 60 градусов вписана окружность с центром O. Радиус окружности равен 5. Найти длину отрезка BO.
Т.к. sin A= cos(90-A), то sin∠BMC = cos∠BMO, В прямоугольнике ABCD проведена диагональ AC. Синус угла BAC равен 0,3. Найти косинус угла CAD.
В треугольнике ABC выполняется соотношение AB:BC:CA=2:4:5. Найти cosA.
Ответ: 0,65.