а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC=40°
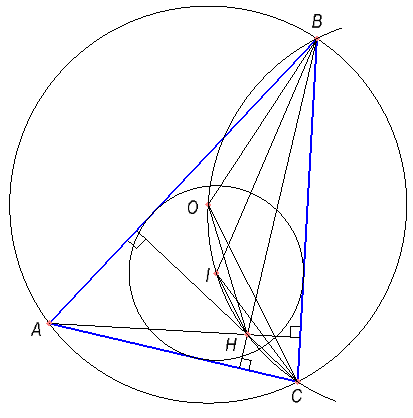
Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC=∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC=70°.
Уникальность ситуации для конкретных данных. Нужно сделать проверку на принадлежность окружности.
Точка O — центр окружности, описанной около остроугольного треугольника ABC. Известно, что ∠BAC=∠OBC+∠OCB. Найти угол BOC.
В треугольнике ABC угол A – 60 градусов. Найти углы между высотами BK и CM.
В треугольнике ABC угол A – 60 градусов, B- 70 градусов. Найти углы между биссектрисами BK и CM.
В треугольнике ABC угол B- 70 градусов. О- центр описанной окружности, I- центр вписанной окружности. Угол OBC – 30 градусов. Найти угол OBI.
Ответ:10º; 5º.
