а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK=3 и MK=12.
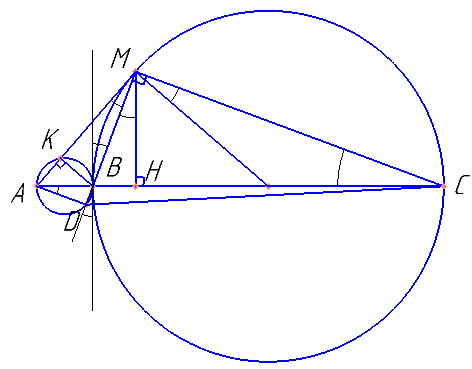
Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK=4 и MK=12.
Общая касательная к двум окружностям дает серию равных углов, из которых легко доказывается пункт а).
Доказать, что диагонали трапеции разбивают ее на 4 треугольника, два из которых равновелики.
Доказать, что треугольники MBK и MBH равны.
На гипотенузе AC прямоугольного треугольника АВС взяли точку М так, что AM=3, MC=12. CB=12. Из точки М построили перпендикуляр, который пересекает АВ в точке К. Найти МК.
Ответ:.30; \( \frac{96}{\sqrt{7}} \).
