Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN=4 и AM:MC=1:3.
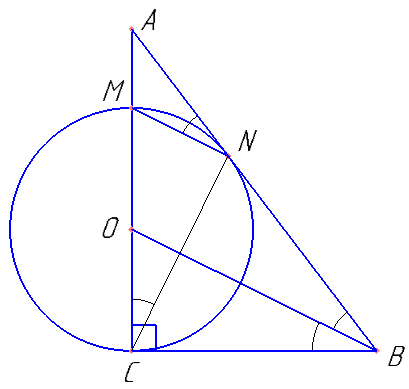
Доказать, что CN перпендикулярно OB. Накрест лежащие прямые углы доказывают пункт а).
Окружность с радиусом АС пересекает АВ — гипотенузу прямоугольного треугольника АВС в точке M. ВМ:МА = 2:3. Найти ВС:ВМ.
Дан один размер и отношение отрезком — пытаемся решить через подобие треугольников. Обозначим MA за x. Лучше за x брать самый маленький отрезок. Выразить через x — MC, MN, AN — из соотношения отрезков касательной и секущей. Обосновать подобие треугольников AMC и ANC. Составить соотношение подобия, найти x.
Найти OB, высоту трапеции BOMN, площадь трапеции.
Ответ: 7.
