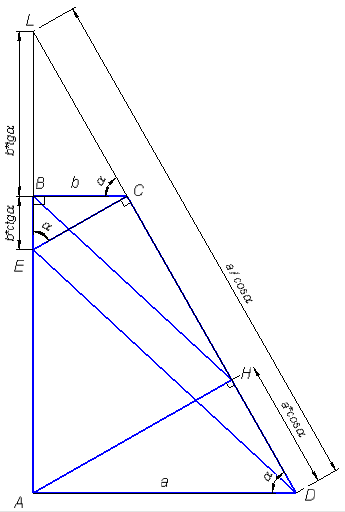
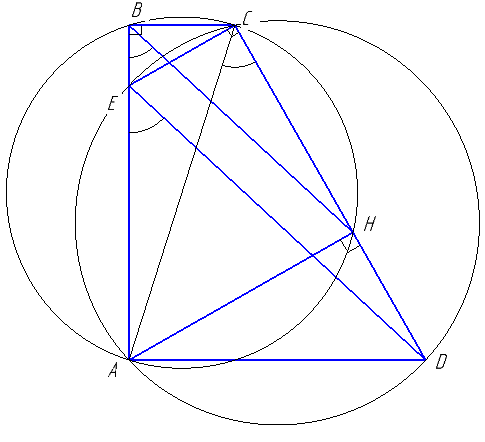
В трапеции ABCD боковая сторона AB перпендикулярна основаниям. Из точки A на сторону CD опустили перпендикуляр AH. На стороне AB отмечена точка E так, что прямые CD и CE перпендикулярны.
а) Докажите, что прямые BH и ED параллельны.
б) Найдите отношение BH к ED, если ∠BCD=120°.
Если доказать, что отрезки LB, LH пропорциональны отрезкам LE, LD, то из подобия треугольников пункт а) доказан.
Пункт а) также легко доказывается из равенства вписанных углов.
Пункт б) легко рассчитывается из подобия треугольников BLH и ELD.
Доказать, что
\( \frac{tg\alpha}{tg\alpha+ctg\alpha}=(\frac{1}{cos\alpha}-cos\alpha):\frac{1}{cos\alpha} \)
Ответ: 0,75.