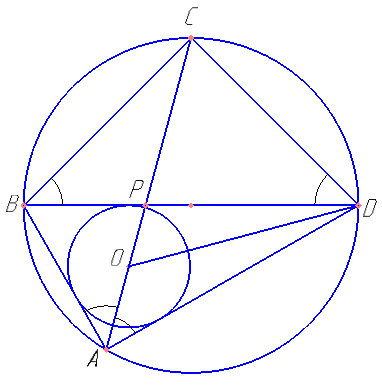
Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что \( \frac{AB}{BC}=\frac{AP}{PD} \).
б) Найдите площадь треугольника COD, где O — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB=5, а BC=\( 5\sqrt{2} \).
В прямоугольном треугольнике катет в два раза меньше гипотенузы. Найти острые углы треугольника.
Если точно построить, то можно заметить, что COD – равносторонний, что доказывается… O – лежит на пересечении биссектрис.
В прямоугольный треугольник АВС, с прямым углом С вписана окружность с центром О. АВ=10, СА=5. Найти угол СВО.
Ответ 12,5\( \sqrt{3} \)
