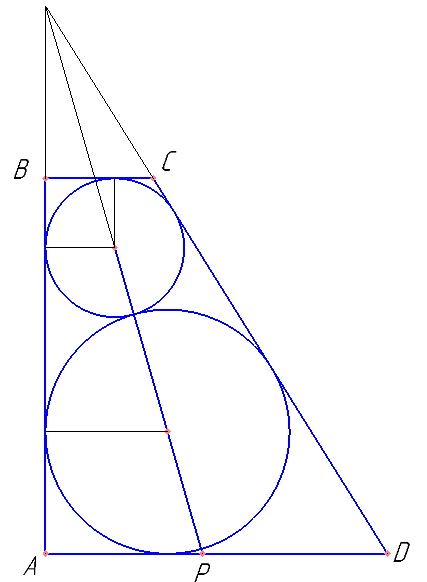
а) Прямая, проходящая через центры окружностей пересекает основание AD в точке Р. Докажите \( \frac{AP}{PD}=\sin {D} \)
б) Найдите площадь трапеции, если радиусы окружностей равны \( \frac{4}{3} , \frac{1}{3} \)
В прямоугольной трапеции АВСD с прямым углом при вершине А расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания и первой окружности.
а) Прямая, проходящая через центры окружностей пересекает основание AD в точке Р. Докажите \( \frac{AP}{PD}=\sin {D} \)
б) Найдите площадь трапеции, если радиусы окружностей равны 2 и 1.
В треугольнике АВС построена биссектриса АК. \( \frac{BK}{KC}=\frac{2}{5} \). AB=3. Найти АС.
В прямоугольной трапеции основания равны 1 и 2, а большая боковая сторона -3. Найти меньшую сторону и косинус острого угла.
Найти \( tg2 \alpha \),, если \( sin \alpha = \frac{1}{3} \).
Ответ: \( \frac{88}{7} \), \( \frac{80+54\sqrt{2}}{7} \).
