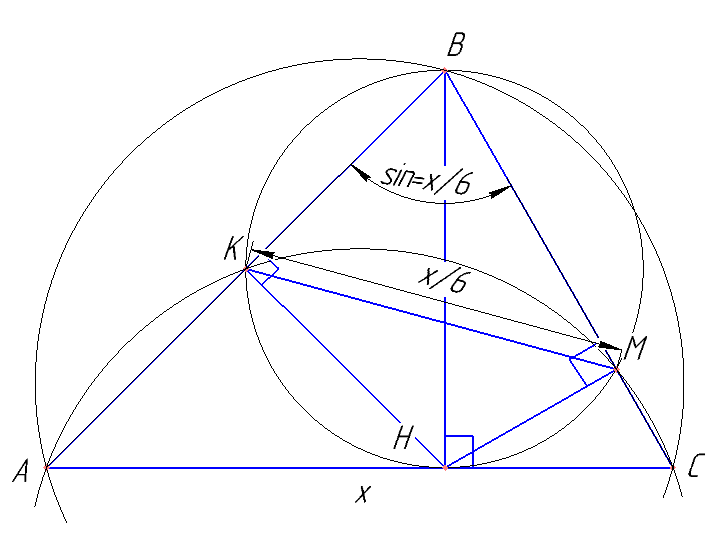
а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH=1, а радиус окружности, описанной около треугольника ABC, равен 3.
Четырехугольник ABCD вписан в окружность. Углы A и C прямые. AC=3, BD=8. Найти радиус окружности.
Треугольник ABC вписан в окружность радиуса 3. AC=x. Найти \( sin B \).
Треугольник BKM вписан в окружность радиуса 0,5. \( sin B = \frac{1}{6} \). Найти KM.
Если соответственные стороны подобных треугольников относятся как 1:6. Как относятся площади этих треугольников?
Треугольник разделен отрезком на 2 части. Площадь меньшей части относится к площади всего треугольника как 1:36. Как относится площадь меньшей части к большей?
Ответ:\( \frac{1}{35} \)
