а) Докажите, что ∠BB1C1 = ∠BAH.
б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если B1C1 = 10 и ∠BAC = 60°.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠BB1C1 = ∠BAH.
б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если B1C1 = 9 и ∠BAC = 30°.
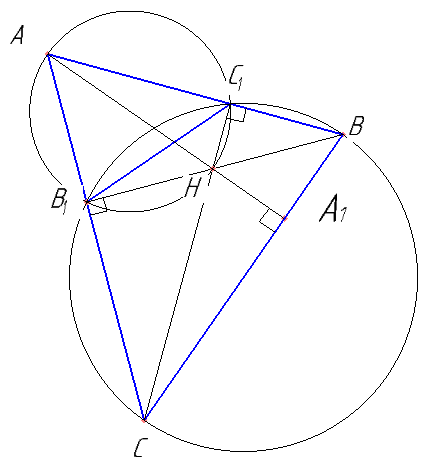
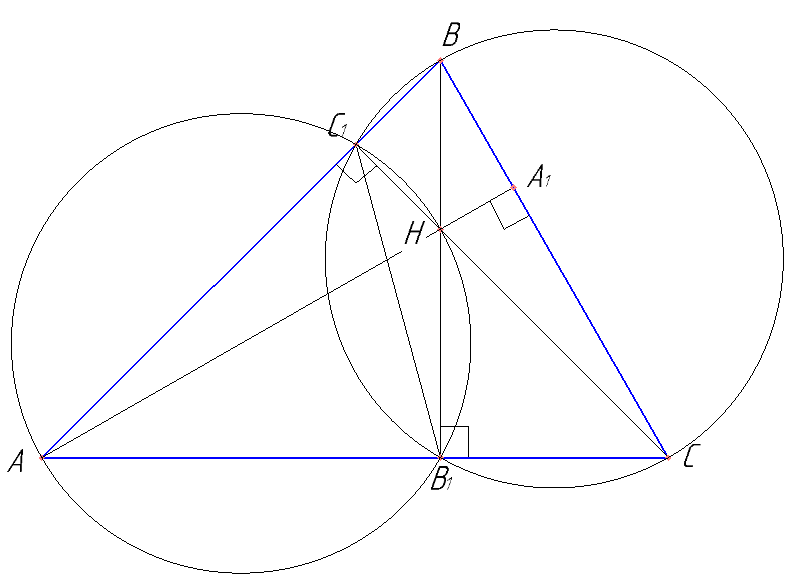
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. Прямая АН пересекает сторону ВС в точке А1. Найти угол АА1В.
Построить дополнительные окружности. Найти равные вписанные углы.
BB1 и CC1 — высоты остроугольного треугольника ABC. Доказать, что треугольник АВ1С1 и ABС подобны.
BB1 и CC1 — высоты остроугольного треугольника ABC. Угол А — 60°. Определить коэффициент пропорциональности отрезков АС, АВ отрезкам и АС1 и АВ1. Найти ВС.
Треугольник АВС вписан в окружность. Угол A равен 30°. BC = 5. Найти радиус окружности.
Треугольник АВС вписан в окружность с радиусом 5. Угол A равен 30°. Найти расстояние между центром окружности и стороной BC.
Ответ:10, 9.
