В пирамиду, в основании которой лежит ромб с острым углом \( \alpha \) и стороной \( \sqrt{6} \), вписана сфера диаметром 1. Найдите угол \( \alpha \) , если известно, что все боковые грани пирамиды наклонены к плоскости её основания под углом 60°.
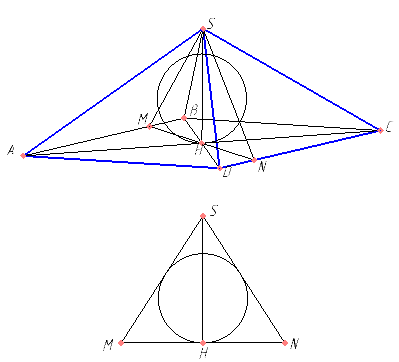
SM и SN — высоты соответствующих граней. Тогда треугольник SMN — равносторонний. Длина его стороны — высота ромба.
В правильный треугольник вписана окружность диаметром 1. Найдите сторону треугольника.
У ромба со стороной \( \sqrt{6} \) и высотой \( \sqrt{3} \) найти острый угол.
Ответ: 45º.
