Объем треугольной призмы ABCA’B’C’ с основанием ABC и боковыми ребрами AA’, BB’, CC’ равен 72. Найдите объем тетраэдра DEFG, где D центр грани ABB’A’, E — точка пересечения медиан треугольника A’B’C’, F — середина ребра AC, G — середина ребра BC.
Объем искомого тела можно находить в лоб по формуле, или как сумму объемов тел из которых оно состоит, или как разность объемов тел , или комбинацией этих способов.
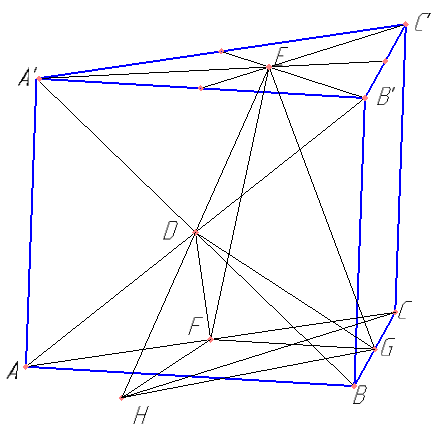
В данном случае удобно достроить заданный тетраэдр до пирамиды EHFG. Площадь основания которого составляет \( \frac{5}{12} \)площади основания призмы, а высоты совпадают. Следовательно, его объем равен \( \frac{5}{36} \) исходного., т. е. 10.
Т.к. основания у пирамид EHFG и DHFG совпадают, а высота в два раза меньше, то и объем в 2 раза меньше.
Ответ: 5.
