Середины сторон выпуклого четырехугольника ABCD лежат на окружности. Известно, что AB=1, BC=4, CD=8. Найдите AD.
Стройте чертеж в соответствии с условием как можно более точно — это ключ к решению.
Следует знать, что фигура соединяющая середины любого, даже не выпуклого , четырехугольника является параллелограммом.
Параллелограмм вписанный в окружность является прямоугольником. Затем я начала строить высоты из вершин и поняла, что они пересекаются в одной точке.
Не бойтесь вводить много переменных.
\( a^2+b^2=0,25 \)
\( b^2+c^2=4 \)
\( c^2+d^2=16 \)
\( d^2+a^2=x^2 \)
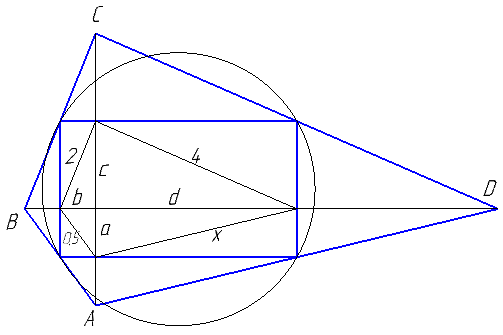
Ответ: 7.
