Дан параллелепипед ABCDA’B’C’D’ с основаниями ABCD и A’B’C’D’ и боковыми ребрами AA’, BB’, CC’, DD’. Все ребра параллелепипеда равны. Плоские углы при вершине B также равны. Известно, что центр сферы описанной около тетраэдра AB’CD’, лежит в плоскости AB’C. Радиус этой сферы равен 2. Найдите длину ребра параллелепипеда.
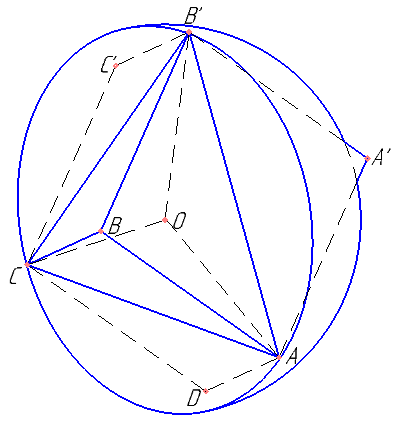
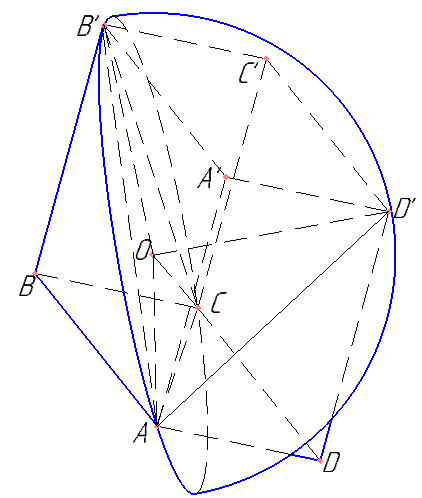
Задача на пространственное воображение. Вместо сферы я взяла для наглядности полусферу. Фраза «Плоские углы при вершине B также равны» — подсказка, что эти углы тупые.
Сначала я поняла, что все грани -одинаковые ромбы. Потом построила в голове 1-ый неполный чертеж, и стало ясно, что одна диагональ ромба (например — AB’) — сторона правильно вписанного в окружность треугольника. Чему равна сторона правильного вписанного треугольника в окружность радиуса 2?
Затем выстроился 2-ой чертеж и пришло понимание, что вторая диагональ ромба (например — AD’) — гипотенуза прямоугольного треугольника с катетами 2.
Найти сторону ромба с известными диагоналями не должно вызывать трудностей. Можно и в уме посчитать.
Построить реальные чертежи для этой задачи оказалось сложнее, чем ее решить.
Ответ: \( \sqrt{5} \)
