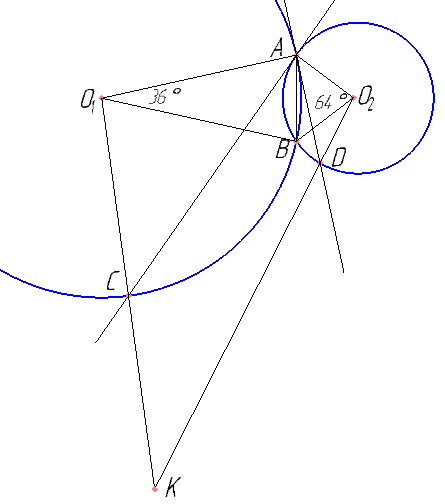
Окружность Ω1 с центром O1 пересекает окружность Ω2 с центром O2 в точках A и B. При этом точки O1 и O2 лежат вне Ω2 и Ω1 соответственно. Касательная к окружности Ω2 в точке A пересекает Ω1 в точках A и C. Касательная к окружности Ω1 в точке A пересекает Ω2 в точках A и D. Найдите угол между прямыми O1C и O2D, если известно, что \( \angle{AO_1B}=36° \) и \( \angle{AO_2B}=64° \).
Задача простая, на мой взгляд, — последовательный подсчет углов.
Треугольники AO1B и AO2B равнобедренные. Найти углы при основаниях. Найти угол O1АO2.
Найти угол BAD и, аналогично, угол BAC. Пригодится теорема об угле между хордой и касательной.
Найти угол BO1C и угол BO2D. Легко посчитать углы AO1C и AO2D. Сумма углов выпуклого четырехугольника…
Ответ: 30°