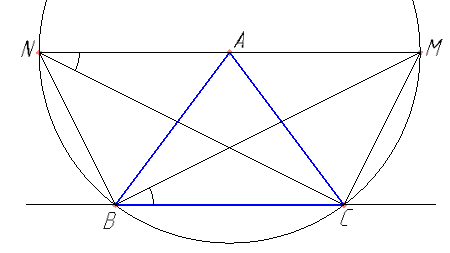
Дан остроугольный треугольник ABC. Биссектриса внутреннего угла при вершине B пересекает биссектрису внешнего угла при вершине C в точке M, а биссектриса внутреннего угла при вершине C пересекает биссектрису внешнего угла при вершине B в точке N.
а) Докажите, что \( \angle CNM=\angle MBC. \)
б) Найдите CN, если AB=AC=15, BC=18.
Угол \( \angle CNM \) и угол \( \angle MBC \) опираются на один отрезок. Если они равны, то точки B, N, M, C должны принадлежать одной окружности. Докажем это. Чему равен угол между биссектрисами смежных углов?
Докажем, что точка A — середина NM. Пойдем от обратного. Допустим, что точка O — середина NM — центр окружности — отличная от A. Но тогда получается, что существует два различных треугольника с равной стороной и двумя примыкающими углами, что невозможно. Следовательно точки A и O совпадают.
Пусть \( \alpha=\angle ABC. \) Тогда -\( sin(\angle NBC)=sin(90+\frac{\alpha}{2})= cos(\frac{\alpha}{2})=\sqrt{\frac{1+cos{\alpha}}{2}} \) \( cos \alpha \) найти очень просто — отношение прилежащего катета к гипотенузе. И теорема синусов нам в помощь.
Ответ: \( 12\sqrt{5} \).