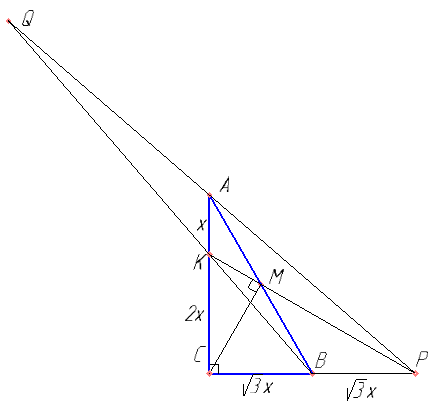
Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC. перепендикулярна CM и пересекает катет AC в точке K. При этом \( AK:KC=1:2 \).
а) Докажите, что угол \( \angle BAC =30° \).
б) Пусть прямые MK и BC пересекаются в точке P, а прямые AP и BK в точке Q. Найдите KQ, если \( BC= 6\sqrt{7} \)
Обоснуйте, почему \( \angle ACM=\angle CAB \).
Треугольник CMK подобен треугольнику ACB. Составьте тождество подобия и выразите через x — MA, MB, MC.
Найдите \( sin A \)
Докажите, что MB — медиана в треугольнике MCP.
По чертежу видно, что QA = AP. Обоснуйте — вспомните теорему Менелая.
Найдите косинус \( \angle {CAP} \) и косинус смежного с ним \( \angle {QAK} \).
Последний шаг — теорема косинусов.
Ответ: \( 28\sqrt{3} \).