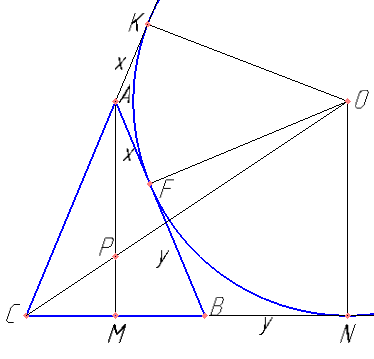
Окружность с центром O касается боковой стороны AB равнобедренного треугольника ABC, продолжения боковой стороны AC и продолжения основания BC в точке N. Точка M — середина основания BC.
а) Докажите, что MN=AC.
б) Найдите OC, если стороны треугольника ABC равны 13, 13, 10.
Очевидно, что \( AC = AB = x + y \). А что следует из \( CK=CN \)?
Точка O равноудалена от сторон CA и CB. Следовательно, CO — … ?
На какие отрезки делит точка P высоту AM?
Треугольники CPM и CON подобны — обоснуйте. Следовательно, CO больше CP во столько же раз во сколько CN больше CM.
Ответ: \( 6\sqrt{13} \)