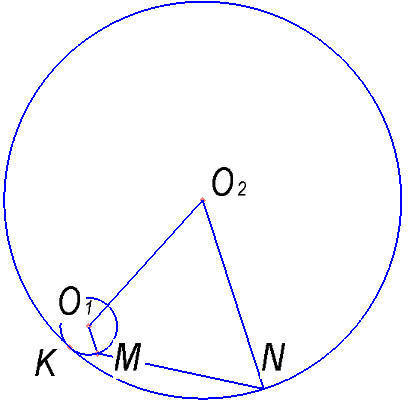
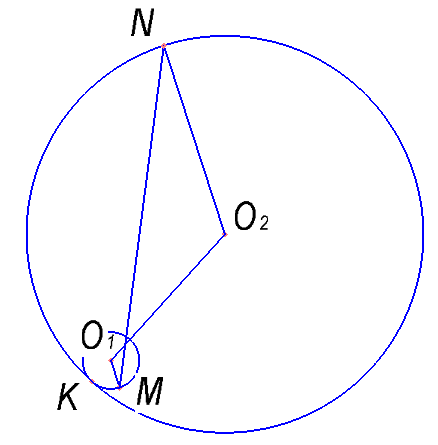
Окружности радиусов 1 и 15 с центрами O1 и O2 соответственно касаются внутренним образом в точке K, MO1 и NO2 — параллельные радиусы этих окружностей, причём угол MO1O2 равен 120°. Найдите MN.
Окружности радиусов 13 и 20 с центрами O1 и O2 соответственно касаются внутренним образом в точке K, MO1 и NO2 — параллельные радиусы этих окружностей, причём угол MO1O2 равен 120°. Найдите MN.
Доказать, что точка касания окружностей и центры окружностей лежат на одной прямой.
Определить длины сторон треугольников KO1M и KO2N.
В трапеции с основаниями 1 и 15 одна из диагоналей равна 14. Найти отрезки на которые ее делит точка пересечения диагоналей.
Две стороны треугольника равны 1 и \( \frac{7}{8} \). Угол между ними 120º. Найти третью сторону.
Ответ:14 или 26; 7 или 37.