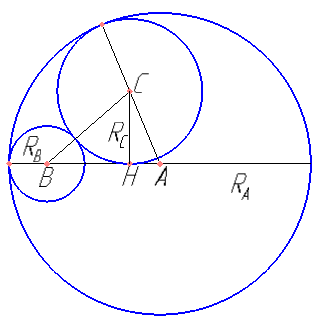
Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трех окружностей равен диаметру наибольшей из этих окружностей.
б) Найдите радиус третьей окружности, если радиусы первых двух равны 4 и 1.
\( AB=R_A-R_B \) \( BC= … \) \( CA= … \)
\( AB+BC+CA = … \)
\( S_{ABC}=\frac{1}{2}AB*CH \)
\( S_{ABC}=\sqrt{p(p-AB)(p-BC)(p-CA)} \)
Ответ: 1,92