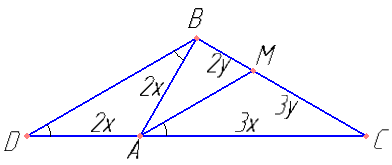
На продолжении стороны AC за вершину A треугольника ABC отложен отрезок AD, равный стороне AB. Прямая проходящая через точку A параллельно BD, пересекает сторону BC в точке M.
а) Докажите, что AM — биссектриса \( \angle BAC \).
б) Найдите площадь трапеции AMBD, если площадь треугольника ABC равна 180 и известно отношение AC : AB = 3 : 2.
Простые вопросы, которые все знают — Какие углы называются соответственными? Чему равен внешний угол треугольника? Пункт а доказан.
По теореме Фалеса BM : MC = 2 : 3.
Если площадь треугольника ABC равна 180, то чему равна площадь треугольника AMC? А треугольника DBC? Если затрудняетесь, то поможет формула площади треугольника через синус.
Ответ: 192.