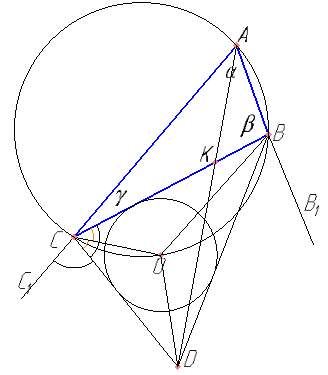
Биссектрисы внешних углов B и C треугольника ABC пересекаются в точке D. Центр окружности вписанной в треугольник BCD, лежит на окружности, описанной около треугольника ABC.
а) Докажите, что \( \angle ABC=60° \)
б) Найдите синус угла между прямыми AD и BC, если AB=3, AC=8.
В таком случае, я советую ввести много переменных и составлять с ними уравнения, системы уравнений. Помните свойства углов вписанного четырехугольника? Выразите через \( \gamma \) угол \( \angle ACO \)?
Найти \( \alpha \) из: \( \ \begin{cases} 45°+\frac{3\gamma }{4}+45°+\frac{3\beta }{4}=180°\\ \gamma +\beta =180°-\alpha \end{cases} \) .
Легко найти СB, используя теорему косинусов.
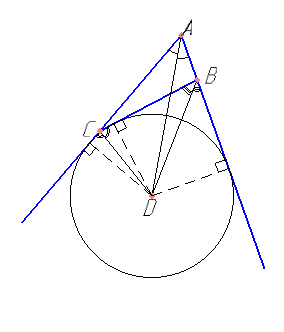
Если составить точный чертеж, то похоже, что AD — биссектриса. Для доказательства понадобится второй чертеж и понимание, что точки равноудаленные от сторон угла лежат на биссектрисе. Точка D равноудалена от AC1, CB, AB1. Следовательно, AD — биссектриса и \( \angle CAD= 30° \).
Внешний угол треугольника равен сумме двух не смежных с ним углов треугольника, т.е. \( \angle AKB= \gamma +30° \)
Тригонометрия — вспомните формулу синуса суммы двух углов. Надеюсь, что посчитать \( sin\gamma, cos\gamma \) не составит труда.
Ответ: \( \frac{11}{14} \)