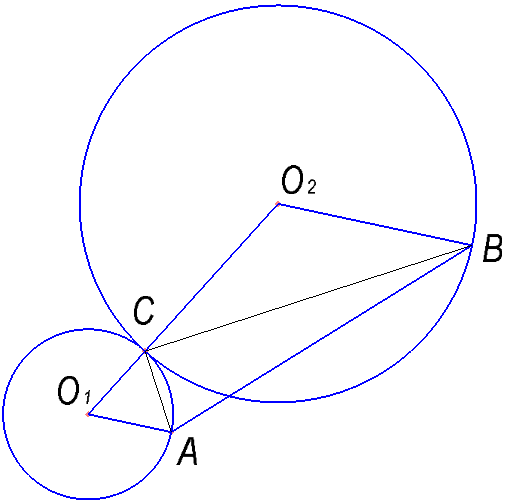
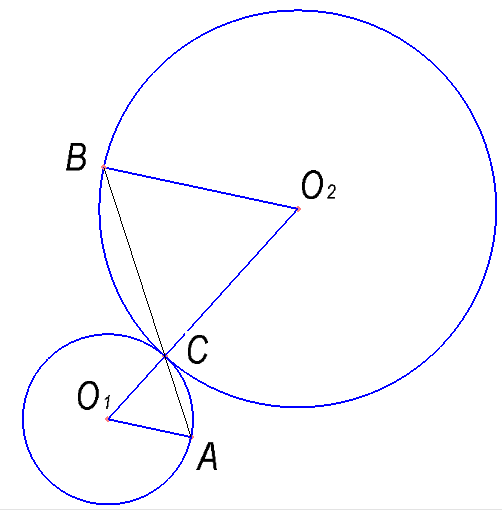
Окружности радиусов 13 и 20 с центрами O1 и O2 соответственно касаются внешним образом в точке C, AO1 и BO2 — параллельные радиусы этих окружностей, причём угол AO1O2 равен 60°. Найдите AB.
Окружности радиусов 13 и 35 с центрами O1 и O2 соответственно касаются внешним образом в точке C, AO1 и BO2 параллельные радиусы этих окружностей, причём угол AO1O2 равен 60°. Найдите AB.
В трапеции ABCD на боковой стороне AB взята точка M так, что AM=AD, MB=BC. Доказать, что угол DMC прямой.
В равнобедренном треугольнике с боковыми сторонами равными 3 и углом между ними — 120º — найти основание.
В трапеции ABCD с основаниями AD и BC на диагонали AС взята точка M так, что AM=AD, MB=BC. Доказать, что диагонали трапеции пересекаются в точке M.
Ответ: 37 или 33; 62 или 48.