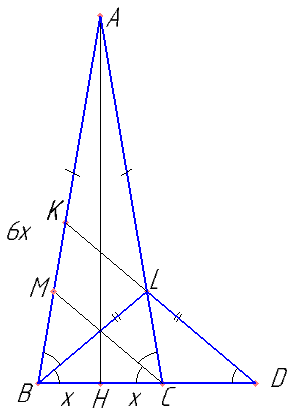
На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник BCL равнобедренный.
б) Известно, что \( cos\angle ABC=\frac{1}{6} \). В каком отношении прямая DL делит сторону AB?
Дополнительное построение второй биссектрисы CM сильно облегчает доказательство пункта а). Докажите, что \( \angle MCL=\angle CLD \)
Есть прекрасный прием — если известен косинус угла, например \( \frac{2}{3} \), то катет и гипотенузу можно обозначить за \( 2x \) и \( 3x \).
Выразите через x AL и LC, используя свойство биссектрисы треугольника.
Выразите через x отрезки AL, LC, CD. Вспомните теорему Менелая.
Ответ: \( \frac{AK}{KB}=\frac{9}{7} \)