Окружности радиусов 9 и 15 с центрами O1 и O2 соответственно касаются в точке L. Прямая, проходящая через точку L, вторично пересекает меньшую окружность в точке K, а большую — в точке M. Найдите площадь треугольника KMO1, если угол LMO2 равен 15°.
Окружности радиусов 4 и 13 с центрами O1 и O2 соответственно касаются в точке L. Прямая, проходящая через точку L, вторично пересекает меньшую окружность в точке K, а большую — в точке M. Найдите площадь треугольника KMO1, если угол LMO2 равен 22,5°.
Формулы площади треугольника.
Найти: sin 135°, sin 120°.
В окружности с центром О и радиусом 9, находится треугольник АОВ. Точки А и В лежат на окружности, угол ОАВ равен 15°. Найти длину стороны АВ.
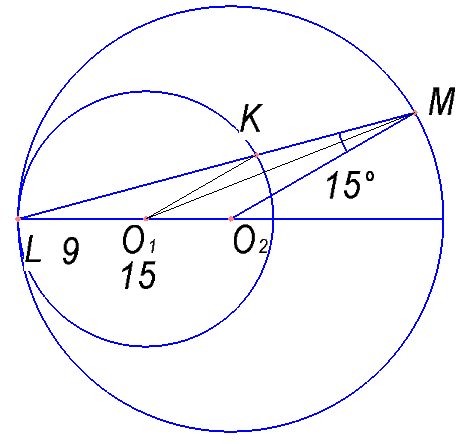
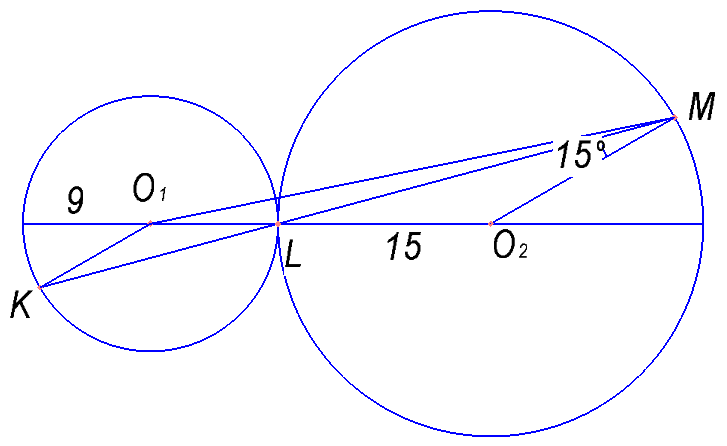
Ответ: 9\( \sqrt{2} \) или 17\( \sqrt{2} \) ; 13,5 или 54.
