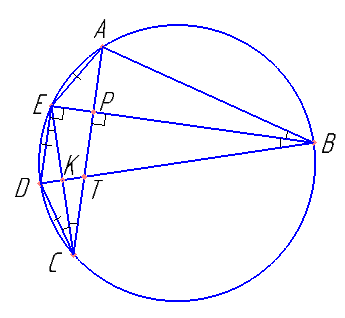
Точки A, B, C, D, E лежат на окружности в указанном порядке, причем AE=ED=CD, EB\( \perp \)AC. Отрезки AC и BD пересекаются в точке T.
а) Доказать, что прямая EC пересекает отрезок TD в его середине.
б) Найдите площадь ABT, если BD=10, AE=\( 2\sqrt{2} \).
Определить тип четырехугольника ACDE.
Обоснуйте равенство углов на чертеже.
Докажите, что DB — диаметр.
Найдите треугольник подобный TCK. И обоснуйте, что угол K прямой.
Обоснуйте равенство треугольников TCK и DCK.
Найдите \( sin\angle ACE \). Найти DK, KT, TB.
Если \( sin \alpha=\frac{\sqrt2}{5} \), найти \( sin 2\alpha. \)
В равнобедренном треугольнике боковые стороны равны 8,4. Синус угола между ними \( \frac {2\sqrt{46}}{25} \). Найти площадь треугольника.
Ответ: \( \frac{1764\sqrt{46}}{625} \)