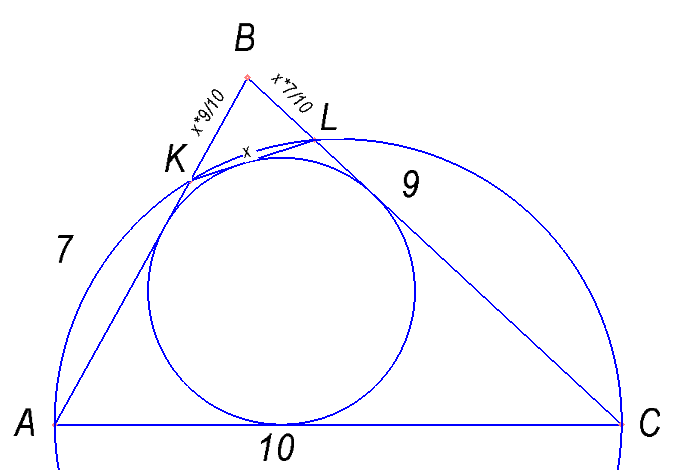
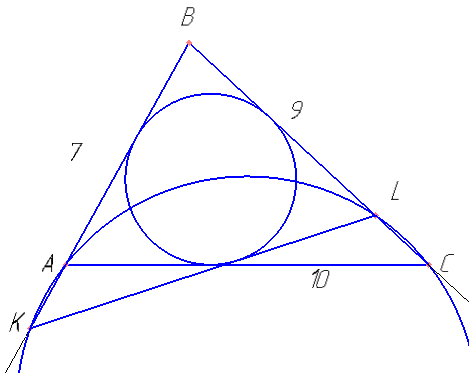
В треугольнике ABC известны стороны: AB=7, BC=9, AC=10. Окружность, проходящая через точки A и C, пересекает прямые BA и BC соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.
Доказать, что треугольник BKL подобен BCA. Ввести переменную, выразить через нее стороны треугольника BKL.
Используя свойство сторон описанного четырехугольника, составить уравнение и найти KL.
Доказать, что треугольник KBL подобен треугольнику CBA.
Доказать, что, если у подобных треугольников радиус вписанной окружности равен, то такие треугольники равны.
Ответ: \( \frac{30}{13} \) или 10.