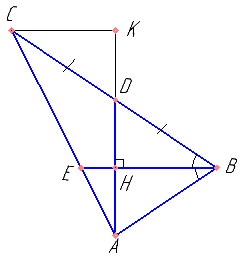
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 32. Найдите стороны треугольника ABC.
Определить тип треугольника DAB. Чему равно DH?
Пусть CK||EB. Доказать, что треугольник CKD равен треугольнику BHD.
Пусть HB=x, тогда EH=32-x. Выразите через x площадь треугольника ABC, как сумму площадей треугольников ECB и EAB. Выразите через x площадь треугольника ABC, как сумму площадей треугольников ACD и ABD.
Решить уравнение \( \frac{1}{2}*32*32+\frac{1}{2}*32*16 = \frac{1}{2}*32*x+\frac{1}{2}*32*x \).
В поиске длин сторон треугольника ABC поможет теорема Пифагора.
Ответ: \( 8\sqrt{13}, 16\sqrt{13}, 24\sqrt{5} \):