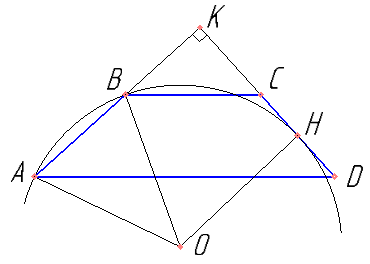
В трапеции ABCD основания AD и BC равны соответственно 49 и 21,
а сумма углов при основании AD равна 90º. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Обосновать подобие треугольников AKD и BKC. Найти BK.
Используя теорему о касательной и секущей найти KH.
В прямоугольной трапеции AKHO угол K равен 90º. Известно, что большее основание \( AK=35 \), \( KH=5\sqrt{21} \), \( AO=OH \) . Найти \( AO \).
Ответ: 25