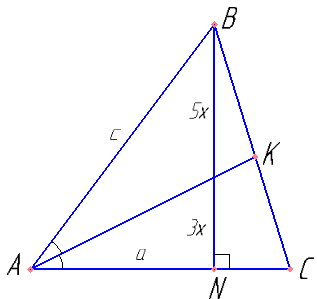
В треугольнике ABC биссектриса угла A делит высоту, проведённую
из вершины B, в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
Если нужен радиус описанной окружности, то пригодится теорема синусов.
Используя свойство биссектрисы можно найти \( \frac{a}{c} \), т.е. \( cos A \)
Найти \( sin A \) поможет основное тригонометрическое тождество.
Ответ: 5