Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=10, а углы B и C четырёхугольника равны соответственно 112º и 113º.
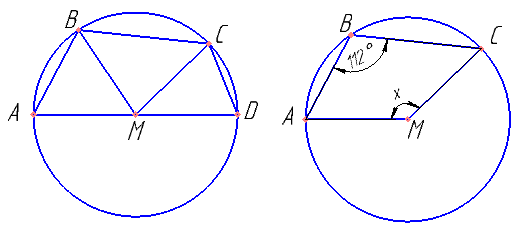
В четырехугольнике ABCM вершины A, B и C принадлежат окружности, а точка M — центр этой окружности. Угол B равен 112º. Найти угол M.
Найти углы CMA, CMD, BMD, BMA, BMC.
В равнобедренном прямоугольном треугольнике гипотенуза равна 10. Найти катеты.
Ответ: \( 10\sqrt{2} \)
