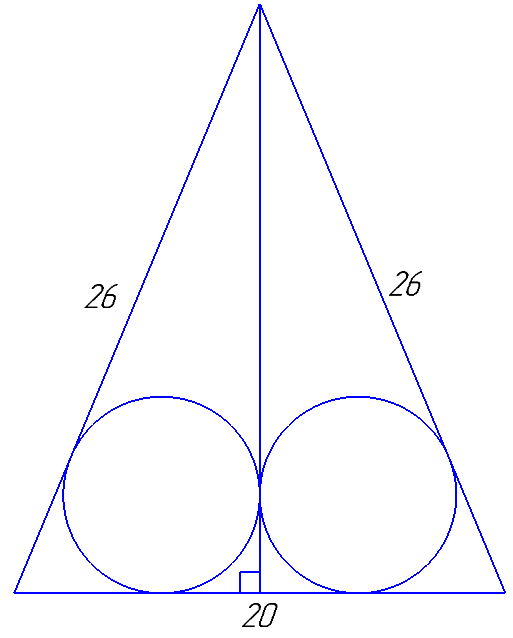
Дан треугольник со сторонами 26, 26 и 20. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
На пересечении чего лежит центр вписанной окружности ?
Найти радиус вписанной окружности, треугольника со сторонами 10, 26, 26.
Найти радиус вписанной окружности, треугольника со сторонами 20, 26, 26.
У двух подобных треугольников коэффициент подобия — k. Как относятся соответственные высоты этих треугольников?
В треугольник с основанием 26 и высотой \( \frac{20}{3} \) вписан прямоугольник, у которого большая сторона лежит на основании треугольника и в 2 раза больше меньшей. Составить тождество подобия треугольников с участием высот. Найти стороны прямоугольника.
Ответ: 4 или \( \frac {260}{59} \)
