В правильной четырехугольной пирамиде SABCD сторона основания равна 4. а боковое ребро равно 7. На ребрах AB и SB отмечены точки M и K соответственно, причем AM=SK=1. Точки M и K принадлежат плоскости α, которая перпендикулярна плоскости ABC.
а) Докажите, что плоскость α содержит точку C.
б) Найдите площадь сечения пирамиды SABCD плоскостью α.
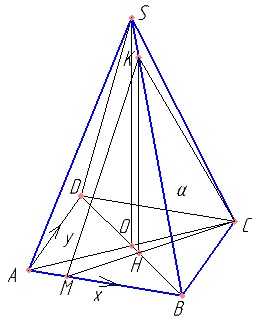
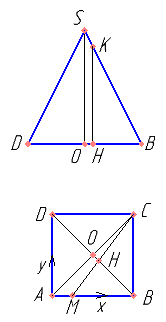
Построение сечения: \( AM=\frac{1}{4} AB \) ,\( SK=\frac{1}{7} SB \) . KH || SO.
Т.к. треугольники OSB и HKB подобны (обоснуйте), то \( \vec{BH}=\frac{6}{7}\vec{BO} \). \( \vec{MH}=\vec{MB}+\vec{BH} \). Найти координаты точек A, B, C, O. Найти координаты векторов \( \vec{MH} \) и \( \vec{MC} \).
Докажите, что вектора \( \vec{MH}(\frac{9}{7};\frac{12}{7}) \) и \( \vec{MC}(3; 4) \) коллинеарны.
Найти MC, HK, площадь треугольника MKC.
Ответ:\( \frac{15\sqrt{41}}{7} \)
