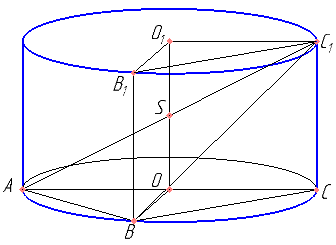
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A и B, а на окружности другого основания — точки B1 и C1, причём BB1 — образующая цилиндра, а отрезок AC1 пересекает ось цилиндра.
а) Докажите, что угол ABC1 прямой.
б) Найдите площадь боковой поверхности цилиндра, если AB=20, BB1=15, B1C1=21.
Построим диаметр AC. Т.к. треугольники ASO и C1SO1 равны (по какому признаку?), то AS=SC1. Из подобия треугольников ASO и AC1C (признак?) следует, что СС1 || OS, т.е. CC1 — образующая и CC1 перпендикуляр к плоскости основания.
Обоснуйте, что треугольник ABC — прямоугольный.
Можно ли применить для доказательства пункта а) теорему о трех перпендикулярах?
Верно ли, что развертка боковой поверхности цилиндра — прямоугольник?
Ответ: 435π