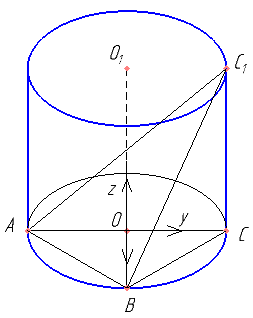
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C1, причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что ∠ACB=45°, AB=\( 2\sqrt{3} \), CC1=\( 2\sqrt{6} \).
а) Докажите, что угол между прямыми AC1 и BC равен 60°.
б) Найдите расстояние от точки B до прямой AC1.
Обоснуйте, что треугольник ABC прямоугольный и равнобедренный. Найти AC, BC.
Найти координаты векторов \( \vec{AC_1}, \vec{BC}, \) Найти угол между ними.
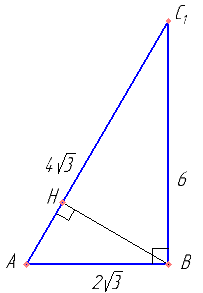
Найти AC1, BC1. Доказать, что треугольник ABC1 — прямоугольный. Найти BH.
Ответ: 3
