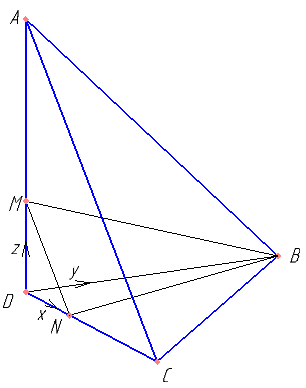
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а AB=BC=AC=\( 6\sqrt{2} \).
а) Докажите, что эта пирамида правильная.
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA=DN:NC=1:2. Найдите расстояние от точки D до плоскости MNB.
Определим координаты точек — C(x,0,0), B(0,y,0), A(0,0,z). Используя равенство \( |\vec{AB}|=|\vec{BC}|=|\vec{CA}|=6\sqrt{2} \) Доказать, что x=y=z. Найти x.
Доказать, что, если одна грань тетраэдра — основание — правильный треугольник, а боковые ребра равны между собой, то такой тетраэдр — правильная пирамида.
Найти DM, DN, DB. Составить уравнение плоскости MNB используя формулу плоскости в отрезках.
Найти расстояние от точки D(0,0,0) до плоскости \( \frac{x}{2}+\frac{y}{6}+\frac{z}{2}=1 \).
Ответ: \( \frac{6}{\sqrt{19}} \)