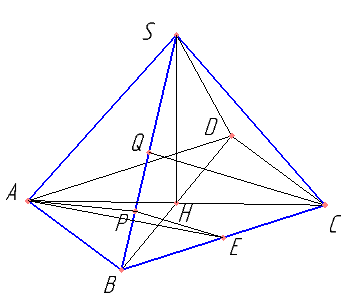
Основанием четырёхугольной пирамиды SABCD является прямоугольник ABCD, причём AB=\( 2\sqrt{2} \), BC=4. Основанием высоты пирамиды является центр прямоугольника. Из вершин A и C опущены перпендикуляры AP и CQ на ребро SB.
а) Докажите, что P — середина отрезка BQ.
б) Найдите угол между гранями SBA и SBC, если SD=4.
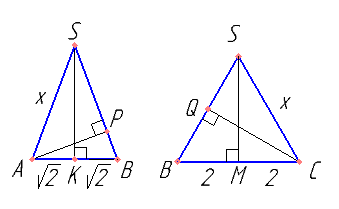
Из треугольника ASB выразить через x — BP. Из треугольника BSC выразить через x — BQ. Поможет подобие треугольников.
PE параллельно QC. Рассчитать PE, PA, AP. Найти \( cos(\angle APE) \).
Ответ: \( arccos(-\frac{5}{\sqrt{21}}) \)
