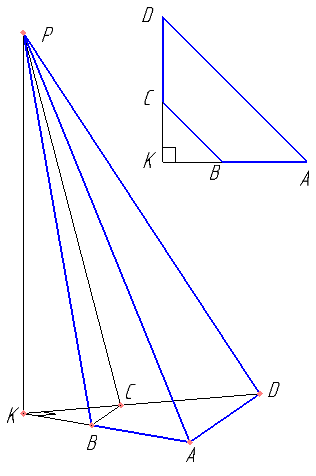
Основанием четырёхугольной пирамиды PABCD является трапеция ABCD, причём ∠BAD+∠ADC=90°. Плоскости PAB и PCD перпендикулярны плоскости основания, K — точка пересечения прямых AB и CD.
а) Докажите, что плоскости PAB и PCD перпендикулярны.
б) Найдите объём пирамиды KBCP, если AB=BC=CD=4, а высота пирамиды PABCD равна 9.
Продолжите теорему: «Если две плоскости, перпендикулярные к третьей плоскости, пересекаются, то их линия пересечения…» Следовательно PK — высота пирамиды.
Т.к. PK, KA и KD взаимно перпендикулярны, то плоскости PAB и PCD ...
Обосновать, что ∠BAD и ∠ADC — углы при основании и, следовательно, трапеция — равнобедренная.
Найти DA. Найти площадь треугольника BKC.
Ответ: 12