На ребре SD правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка M, причём SM:MD=2:1. Точки P и Q — середины рёбер BC и AD соответственно.
а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией.
б) Найдите отношение объёмов многогранников, на которые плоскость MPQ разбивает пирамиду.
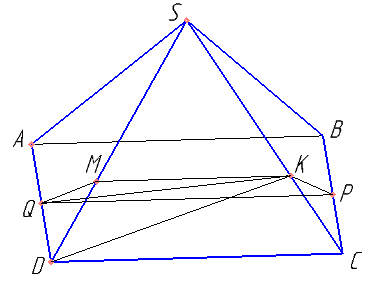
Доказать, что отрезок QP параллелен DC, MK параллелен DC, и QP параллелен MK.
Доказать равенство треугольников DQM и CKP.
Как относятся площади оснований и высоты пирамид KDQPC и SABCD? Чему равен объем пирамиды KDQPC, если объем SАBCD принять на 1?
Чему равен объем пирамиды CADS, если объем SАBCD принять на 1?
Как относятся площади оснований и высоты пирамид KMDQ и CADS, если считать ADS — плоскостью основания? Чему равен объем пирамиды KMDQ, если объем CАDS считать равным \( \frac{1}{2} \)?
Ответ:\( \frac{2}{7} \)
