На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM:MB = CN:NB = 1:2. Точки P и Q — середины рёбер DA и DC соответственно.
а) Докажите, что точки P, Q, M и N лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.
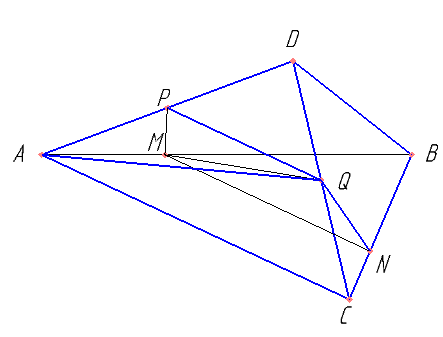
Доказать, что PQ параллельна AC, MN параллельна AC, и PQ параллельно MN.
Можно ли провести плоскость через две параллельные прямые в пространстве?
Как относятся площади оснований и высоты пирамид QAMNC и DABC? Чему равен объем пирамиды QAMNC, если объем DАBC принять на 1?
Как относятся площади оснований и высоты пирамид QAPM и CADB, если считать ADB — плоскостью основания? Чему равен объем пирамиды QAPM, если объем CАDB принять на 1?
Ответ:\( \frac{13}{23} \)
