Боковые стороны KL и MN трапеции KLMN равны 8 и 17 соответственно. Отрезок, соединяющий середины диагоналей, равен 7,5, средняя линия трапеции равна 17,5. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM.
Доказать, что отрезок между серединами диагоналей трапеции равен полуразности оснований.
Найти основания трапеции, если средняя линяя ее равна 17,5, а отрезок, соединяющий середины диагоналей, равен 7,5.
Доказать, что треугольник со сторонами 8, 15, 17 — прямоугольный.
Найти радиус вписанной окружности в прямоугольный треугольник, со сторонами 8, 15, 17.
В прямоугольный треугольник, со сторонами 8, 15, 17 вписана окружность. Найти радиус вписанной окружности у подобного треугольника в котором стороне 10 соответствует сторона 15 исходного.
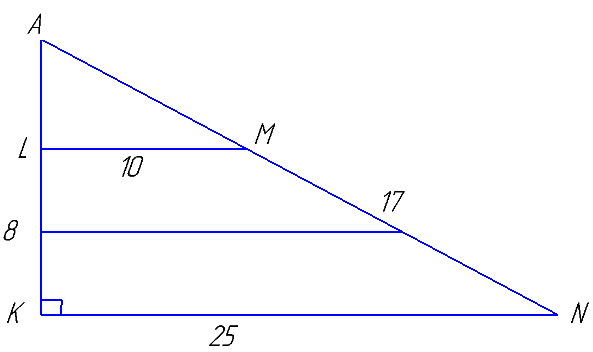
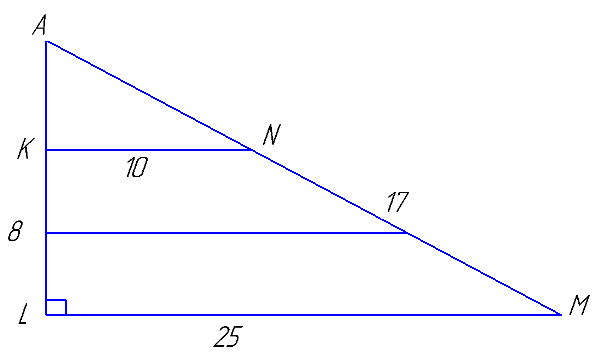
Ответ: 2 или 5.
