В правильной треугольной пирамиде SABC сторона AB основания равна 12, а высота пирамиды равна 1. На рёбрах AB, AC и AS отмечены точки M, N и K соответственно, причём AM=AN=3 и AK=\( \frac{7}{4} \).
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC.
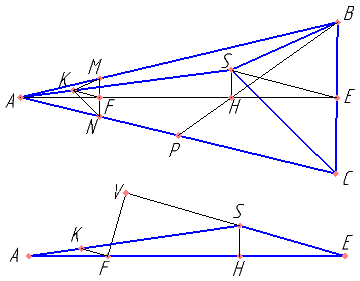
Доказать, что треугольник AKF подобен треугольнику ASE.
Найти две пересекающихся прямых плоскости MNK и две соответственно параллельных им прямых плоскости SBC.
Обосновать, что расстояние от точки M до плоскости SBC равно расстоянию от точки F до прямой SE. Найти \( sin \angle {E} \) Найти FV.
Ответ:\( \frac{9\sqrt{39}}{26} \)
