а) Докажите, что прямые BC и AD параллельны. б) Найдите AD. Четырёхугольник ABCD вписан в окружность радиуса R=8. Известно, что AB=BC=CD=12.
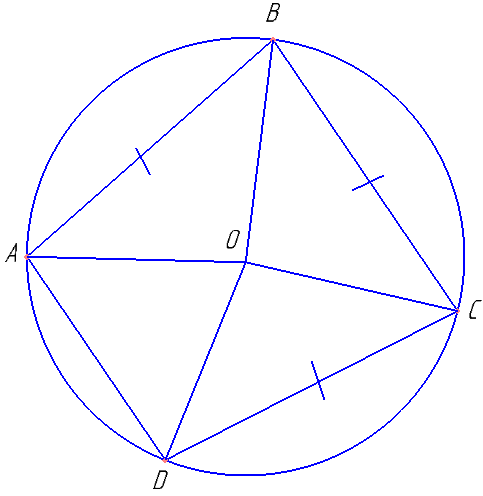
Доказать, что ∠ OAB = ∠ ODC., ∠ OAD = ∠ ODA, ∠ BAD = ∠ CDA, ∠ ABC = ∠ DCB.
Доказать, что ∠DAB+∠ABC=180°. Пригодится теорема об углах вписанного четырехугольника.
Найти \( cos(∠AOB) \)
Найти \( cos(360°-3x) \) , если \( cosx=-\frac{1}{8} \)
Ответ:13,5.
