В правильной четырёхугольной призме ABCDA1B1C1D1 сторона AB основания равна 8, а боковое ребро AA1 равно \( 4\sqrt{2} \). На рёбрах BC и C1D1 отмечены точки K и L соответственно, причём BK=C1L=2. Плоскость γ параллельна прямой BD и содержит точки K и L.
а) Докажите, что прямая A1C перпендикулярна плоскости γ.
б) Найдите расстояние от точки B до плоскости γ.
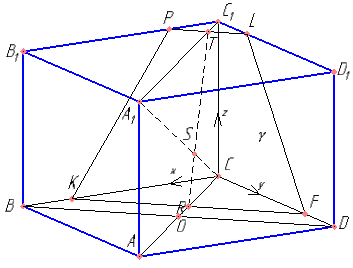
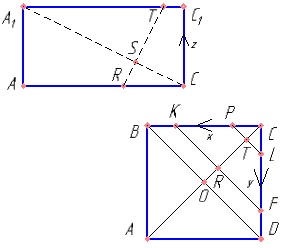
Найти координаты векторов \( \overrightarrow{CA_1} \), \( \overrightarrow{TR} \) и \( \overrightarrow{KF} \) . Доказать, что \( \overrightarrow{CA_1} \) перпендикулярно \( \overrightarrow{TR} \) и \( \overrightarrow{KF} \) .
Составить уравнение плоскости проходящей через точку K(6,0,0) и перпендикулярной вектору \( \overrightarrow{CA_1} (8;8;4\sqrt{2}) \).
Найти расстояние от точки B(8:0:0) до плоскости заданной формулой \( 8x+8y+4\sqrt{2}z-48=0 \).
Ответ: \( 0,4\sqrt{10} \)
