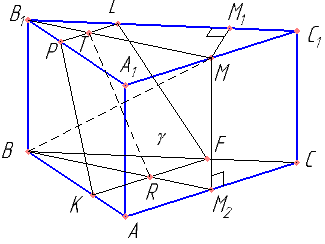
В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 6, а боковое ребро AA1 равно 3. На рёбрах AB и B1C1 отмечены точки K и L соответственно, причём AK=B1L=2. Точка M — середина ребра A1C1. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите объём пирамиды, вершина которой — точка M, а основание — сечение данной призмы плоскостью γ.
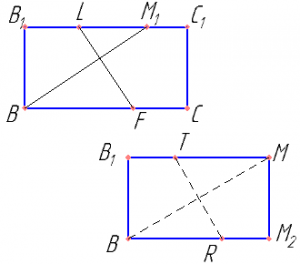
Доказать, что BM1 перпендикулярна LF.
Обоснуйте, что BM перпендикулярна LF, и что BM перпендикулярно KF.
Определить тип четырехугольника KPLF. Найти KF, PL, TR.
Доказать, что отрезки TR и BM точкой пересечения делятся пополам. Найти высоту пирамиды KPLFM.
Ответ:\( 6\sqrt{3} \)
